No, it doesn’t. It never talks about Terms, nor The Distributive Law (which isn’t the same thing as the Distributive Property). These are the 2 rules of Maths which make this 100% not ambiguous.
💡𝚂𝗆𝖺𝗋𝗍𝗆𝖺𝗇 𝙰𝗉𝗉𝗌📱
- 0 Posts
- 87 Comments
Also noted that you’ve declined on taking on that bet I offered.
somewhere
You know EXACTLY where I said those things, and you’ve been avoiding addressing them ever since because you know they prove the point that #MathsIsNeverAmbiguous See ya.
Sources are important not just for what they say but how they say it, where they say it, and why they say it.
None of which you’ve addressed since I gave you the source. Remember when you said this…
you can’t identify authors, you can’t check for bias
So, did you do that once I gave you the link? And/or are you maybe going to address “what they say but how they say it, where they say it, and why they say it” in regards to the link I gave you?
You keep reiterating your point as if it is established fact,
What they teach in Maths textbooks aren’t facts? Do go on. 😂
tell me how it supports you
I did, and you’ve apparently refused to read the relevant part.
in comparison to a Phd
You know not all university lecturers do a Ph.D. right? In which case they haven’t done any more study at all. But I know you really wanna hang on to this “appeal to authority” argument, since it’s all you’ve got.
I have no interest in continuing this discussion
Yeah I saw that coming once I gave you the link to the textbook.
including the ‘highschool’ math
…when they were in high school.
teach the same (or similar) curriculum each and every year
There you go. Welcome to why high school teachers are the expert in this field.
math textbooks as the ultimate solution and so, so many of them are written by professors
So wait, NOW you’re saying textbooks ARE valid in what they say? 😂
I want to point out that your only two sources
All that points out is that you didn’t even read THIS thread properly, never mind the other one. Which two are they BTW? And I’ll point out which ones you’ve missed.
I assume you accepted that seeing as you did not respond to that point
Well, I’ll use your own logic then to take that as a concession, given how many of my points you didn’t respond to (like the textbook that I gave you the link to, and the Cajori ab=(ab) one, etc.).
I’ve given 3 sources,
3 articles you mean.
all of which you dismiss simply because
…all of them have forgotten about The Distributive Law and Terms., which make the expression totally unambiguous. Perhaps you’d like to find an article that DOES talk about those and ALSO asserts that the expression is “ambiguous”? 😂 Spoiler alert: every article, as soon as I see the word “ambiguous” I search the text for “distributive” and “expand” and “terms” - can you guess what I find? 😂 Hint: Venn diagram with little or no overlap.
I could probably find some highschool textbooks that support weak juxtaposition if I searched,
Do you wanna bet on that? 😂
without ever providing a source that explains these rules
They’re in my thread, if you’d bothered to read any further. By your own standards, 😂I’ll take it that you concede all of my points that you haven’t responded to.
I expect you to have a mathematical proof for why weak juxtaposition would never work, one that has no flaws. Otherwise, at best you have a hypothesis
You know some things are true by definition, right, and therefore don’t have a proof? 1+1=2 is the classic example. Or do you challenge that too?
So do YOU have a hypothesis then? How “weak juxtaposition” could EVER work given “strong juxtaposition” is the only type ever used in any of the rules of Maths? I’ll wait for your proof…
without providing evidence for your own position
You know full well it’s all in my thread. Where’s yours?
I’m saying I shouldn’t have to go looking
You didn’t have to go looking - you could’ve just accepted it at face-value like other people do.
You’ve provided a single textbook,
No, multiple textbooks. If you haven’t seen the others yet then keep reading. On the other hand you haven’t provided any textbooks.
the argument is that both sides are valid and accepted
But they’re not. The other side is contradicting the rules of Maths. In a Maths test it would be marked as wrong. You can’t go into a Maths test and write “this is ambiguous” as an answer to a question.
here’s an article from someone who writes textbooks
Not high school textbooks! Talk about appeal to authority.
Yep, seen it before. Note that he starts out with “It is not clear what the textbook had intended with the 3y”. How on Earth can he not know what that means? If he just picked up any old high school Maths textbook, or read Cajori, or read Lennes’ letter, or even just asked a high school teacher(!), he would find that every single Maths textbook means exactly the same thing - ab=(axb). Instead he decided to write a long blog saying “I don’t know what this means - it must be ambiguous”.
Not only that, but he also didn’t know how to handle x/x/x, which shows he doesn’t remember left associativity either. BTW it’s equal to x/x² (which is equal to 1/x).
the ambiguity exists
…amongst people who have forgotten the rules of Maths. The Maths itself is never ambiguous (which is the claim many of them are making - that the Maths expression itself is ambiguous. In fact the article under discussion here makes that exact claim - that it’s written in an ambiguous way. No it isn’t! It’s written in the standard mathematical way, as per what is taught from textbooks). It’s like saying “I’ve forgotten the combination to my safe, and I’ve been unable to work it out, therefore the combination must be ambiguous”.
You are correct, I suppose a mathematics professor from Harvard (see my previous link for the relevant discussion of the ambiguity) isn’t at the high school level.
Thank you. I just commented to someone else last night, who had noticed the same thing, I am so tired of people quoting University people - this topic is NOT TAUGHT at university! It’s taught by high school teachers (I’ve taught this topic many times - I’m tutoring a student in it right now). Paradoxically, the first Youtube I saw to get it correct (in fact still the only one I’ve seen get it correct) was by a gamer! 😂 He took the algebra approach. i.e. rewrite this as 6/2a where a=1+2 (which I’ve also used before too. In fact I did an algebraic proof of it).
the ambiguity exists and one side is not immediately justified/‘correct’
The side which obeys the rules of Maths is correct and the side which disobeys the rules of Maths is incorrect. That’s why the rules of Maths exist in the first place - only 1 answer can be correct (“ambiguity” people also keep claiming “both answers are correct”. Nope, one is correct and one is wrong).
That’s a leading question and is completely unhelpful to the discussion.
Twice I said things about it and you said you didn’t believe my interpretation is correct, so I asked you what you think he’s saying. I’m not going to go round in circles with you just disagreeing with everything I say about it - just say what YOU think he says.
Here you go - I found I did save a screenshot of Cajori saying ab and (ab) are the same thing - I didn’t think I had.

In fact you’re not allowed to add the multiplication - it breaks up the factorised term, hence gives a different answer.
The rule is you’re not allowed to add dots (multiplication) - broke up the factorised term, which is why a different answer.
Only if it’s a fraction. If it’s 2 separate terms then you use whatever your country uses for division - obelus or colon or whatever. They have to be 2 separate things, otherwise how would you write to divide by a fraction?
While I agree the problem as written is ambiguous
It’s not.
the answer pretty much always ends up being something along the lines of “well the experts do this” or “this professor at this prestigious university says this”, or “the scientific community says”.
Agree completely! Notice how they ALWAYS leave out high school Maths teachers and textbooks? You know, the ones who actually TEACH this topic. Always people OTHER THAN the people/books who teach this topic (and so always end up with the wrong conclusion).
while basic education and basic calculators use weak juxtaposition
Literally no-one in education uses so-called “weak juxtaposition” - there’s no such thing. There’s The Distributive Law and Terms, both of which use so-called “strong juxtaposition”. Most calculators do too.
Shouldn’t strong juxtaposition be the precedent and the norm
It is. In fact it’s the rules (The Distributive Law and Terms).
We should start saying weak juxtaposition is wrong
Maths teachers already DO say it’s wrong.
This has been my devil’s advocate argument.
No, this is mostly a Maths teacher argument. You started off weak (saying its ambiguous), but then after that almost everything you said is actually correct - maybe you should be a Maths teacher. :-)
You haven’t provided a textbook that has strong juxtaposition
I told you, in my thread - multiple ones. You haven’t provided any textbooks at all that have “weak juxtaposition”. i.e. you keep asking me for more evidence whilst never producing any of your own.
At best I can search the title of the file you’re in that you also happened to screenshot and hope that I find the right text
I didn’t “just happen” to include the name of the textbook and page number - that was quite deliberate. Not sure why you don’t want to believe a screenshot, especially since you can’t quote any that have “weak juxtaposition” in the first place.
BTW I just tried Googling it and it was the first hit. You’re welcome.
What does matter is that I shouldn’t have to go treasure hunting for your sources.
You don’t - the screenshots of the relevant pages are right there. You’re the one choosing not to believe what is there in black and white, in multiple textbooks.
with differing rules
Yeah, I wrote about inconsistency in textbooks here (also includes another textbook saying you have to expand brackets first), but also elsewhere in the thread is an example where they have been consistent throughout. Regardless of when they remove brackets, in every single case they multiply the coefficient over what’s inside the brackets as the first step (as per BEDMAS, and as per the screenshot in question which literally says you must do it before you remove brackets).
people don’t agree
People who aren’t high school Maths teachers (the ones who actually teach this topic). Did you notice that neither The Distributive Law nor Terms are mentioned at any point whatsoever? That’s like saying “I don’t remember what I did at Xmas, so therefore it’s ambiguous whether Xmas ever happened at all, and anyone who says it definitely did is wrong”.
no such complaint.
So what do you think he is complaining about?
Citation needed.
So you think it’s ok to teach contradictory stuff to them in Maths? 🤣 Ok sure, fine, go ahead and find me a Maths textbook which has “weak juxtaposition” in it. I’ll wait.
Your comments only reference ‘math textbooks’, not anything specific
So you’re telling me you can’t see the Maths textbook screenshots/photo’s?
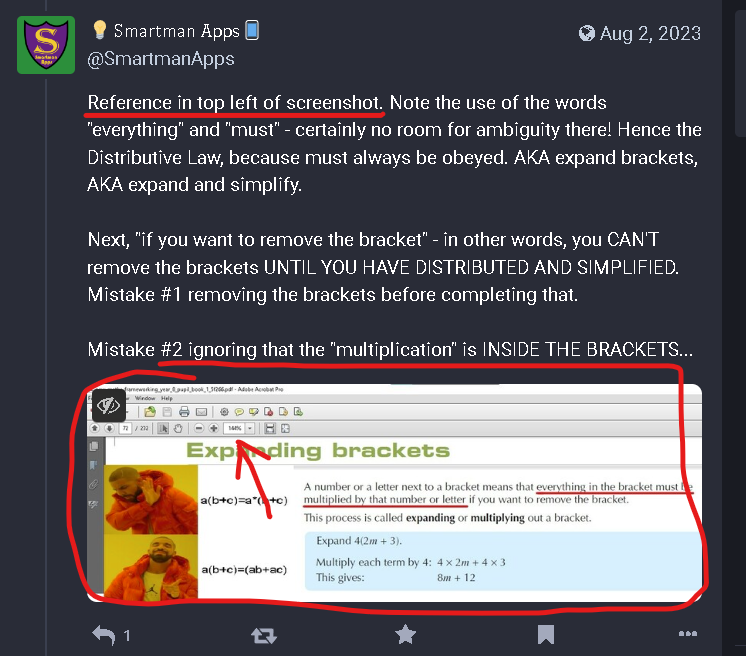
outside of this link which you reference twice in separate comments but again, it’s not evidence for your side, or against it, or even relevant
Lennes was complaining that literally no textbooks he mentioned were following “weak juxtaposition”, and you think that’s not relevant to establishing that no textbooks used “weak juxtaposition” 100 years ago?
We’re talking about x/y(b+c) and whether that should be x/(yb+yc) or x/y * 1/(b+c).
It’s in literally the first textbook screenshot, which if I’m understanding you right you can’t see? (see screenshot of the screenshot above)
you have an uncited refutation of the side you’re arguing against, which funnily enough you did cite.
Ah, no. Lennes was complaining about textbooks who were obeying Terms/The Distributive Law. His own letter shows us that they all (the ones he mentioned) were doing the same thing then that we do now. Plus my first (and later) screenshot(s).
Also it’s in Cajori, but I didn’t find it until later. I don’t remember what page it was, but it’s in Cajori and you have the reference for it there already.
you should probably make it easy to find the evidence you speak of
Well I’m not sure how you didn’t see all the screenshots. They’re hard to miss on my computer!
That doesn’t prohibit them from teaching additional material
Correct, but it can’t be something which would contradict what they do have to teach, which is what “weak juxtaposition” would do.
a single reference
I see you didn’t read the whole thread then. Keep going if you want more. Literally every Year 7-8 Maths textbook says the same thing. I’ve quoted multiple textbooks (and haven’t even covered all the ones I own).
mathematics is a science
Actually you’ll find that assertion is hotly debated.
Regarding your second point I tried to address that in the “distributive property” section,
When I discovered this comment I went to read it, and yes, it’s true you discussed the Distributive Property, however, what these people are talking about is The Distributive Law which isn’t the same thing (though people often call it the wrong name), and makes the question completely unambiguous. You literally can’t move on from the “B”, Brackets, in the rules until there are no brackets left - the B is literally short for “solve Brackets” (every letter is “solve (something)”), and so anyone who does the division before solving the brackets has just violated the order of operations rules.
I’ll take that as an admission that you’re wrong then. Bye now.
P.S. someone else just provided me with even more things which are wrong in it. Even more glad I didn’t waste time reading the rest of it.
Notation isn’t semantics
Correct, the definitions and the rules define the semantics.
Mathematical proofs are working with
…the rules of Maths. In fact, when we are first teaching proofs to students we tell them they have to write next to each step which rule of Maths they have used for that step.
Nobody doubts that those are unambiguous
Apparently a lot of people do! But yes, unambiguous, and therefore the article is wrong.
But notation can be ambiguous
Nope. An obelus means divide, and “strong juxtaposition” means it’s a Term, and needs The Distributive Law applied if it has brackets.
In this case it is: weak juxtaposition vs strong juxtaposition
There is no such thing as weak juxtaposition. That is another reason that the article is wrong. If there is any juxtaposition then it is strong, as per the rules of Maths. You’re just giving me even more ammunition at this point.
Read the damn article
You just gave me yet another reason it’s wrong - it talks about “weak juxtaposition”. Even less likely to ever read it now - it’s just full of things which are wrong.
How about read my damn thread which contains all the definitions and proofs needed to prove that this article is wrong? You’re trying to defend the article… by giving me even more things that are wrong about it. 😂
I stopped reading it when I found it was wrong., and said what was wrong about it. You have still not said where mine is allegedly wrong. I’ll take that as an admission that you’re wrong then.
Ok so you’re saying it never happened, but then in the very next sentence you acknowledge that you know it is happening with TI today
You asked me what I do if my students show me 2 different answers what do I tell them, and I told you that has never happened. None of my students have ever had one of the calculators which does it wrong.
that both behaviors are intentional and documented
Correct. I already noted earlier (maybe with someone else) that the TI calculator manual says that they obey the Primary School order of operations, which doesn’t work with High School order of operations. i.e. when the brackets have a coefficient. The TI calculator will give a correct answer for 6/(1+2) and 6/2x(1+2), but gives a wrong answer for 6/2(1+2), and it’s in their manual why. I saw one Youtuber who was showing the manual scroll right past it! It was right there on screen why it does it wrong and she just scrolled down from there without even looking at it!
none of these calculators is “wrong”.
Any calculator which fails to obey The Distributive Law is wrong. It is disobeying a rule of Maths.
there is no ambiguity where there actually is.
There actually isn’t. We use decimal points (not commas like some European countries), the obelus (not colon like some European countries), etc., so no, there is never any ambiguity. And the expression in question here follows those same notations (it has an obelus, not a colon), so still no ambiguity.
i recommend reading this one instead: The PEMDAS Paradox
Yes, I’ve read that one before. Makes the exact same mistakes. Claims it’s ambiguous while at the same time completely ignoring The Distributive Law and Terms. I’ll even point out a specific thing (of many) where they miss the point…
So the disagreement distills down to this: Does it feel like a(b) should always be interchangeable with axb? Or does it feel like a(b) should always be interchangeable with (ab)? You can’t say both.
ab=(axb) by definition. It’s in Cajori, it’s in today’s Maths textbooks. So a(b) isn’t interchangeable with axb, it’s only interchangeable with (axb) (or (ab) or ab). That’s one of the most common mistakes I see. You can’t remove brackets if there’s still more than 1 term left inside, but many people do and end up with a wrong answer.
By “we” do you mean high school teachers, or Australian society beyond high school?
I said “In Australia” (not in Australian high school), so I mean all of Australia.
Because, I’m pretty sure the latter isn’t true
Definitely is. I have never seen anyone here ever use a colon to mean divide. It’s only ever used for a ratio.
Do you have textbooks where the fraction bar is used concurrently with the obelus (÷) division symbol?
All my textbooks use both. Did you read my thread? If you use a fraction bar then that is a single term. If you use an obelus (or colon if you’re in a country which uses colon for division) then that is 2 terms. I covered all of that in my thread.
EDITED TO ADD: If you don’t use both then how do you write to divide by a fraction?



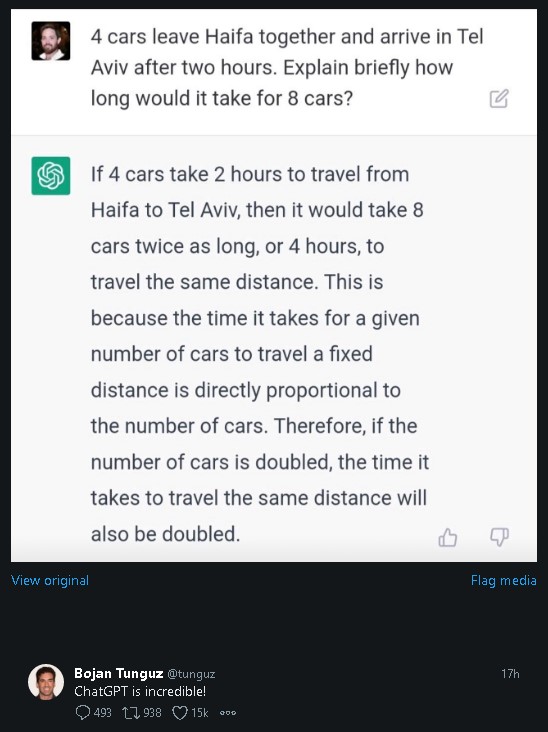
Brackets are ALWAYS first.