You have 20 apples that you put into 5 boxes. “How many apples per box?” 20/5=4. Easy.

You have 20 apples that you put into half a box. “How many apples per box?” 20/0.5=40. You can see how 20 apples in half of a box implies 40 apples per full box.

You have 20 apples that you don’t put into anything. “How many apples per box?” 20/0=? What box? What are you talking about? How can you suggest that there are a number of apples per box when there’s no box to begin with? Lunatic!

You mean that it’s undefined?

You can think of a cake. You can divide a cake into 4 pieces or 2 pieces or basically not divide it, by ‘dividing’ it into 1 piece.

But it’s not possible to divide a cake into 0 pieces. It doesn’t make logical sense. You have to eat it (subtract from it) to actually make 0 pieces. With division, the sum of all pieces has to be 1 cake. If there’s one cake, there’s at least one piece.

What’s confusing is that we have separately decided that ‘dividing’ a cake into 0.5 pieces means you multiply it by 2. So, either 2 cakes or a cake that’s twice as large. That is why some mathematicians do treat 1/0 as ∞.

It is undefined because the inverse of division is multiplication. If you multiply by zero, every answer is zero. If you try to invert that operation you can’t know which number was multiplied by zero to get zero because multiplying by zero doesn’t produce a unique answer for each operation.

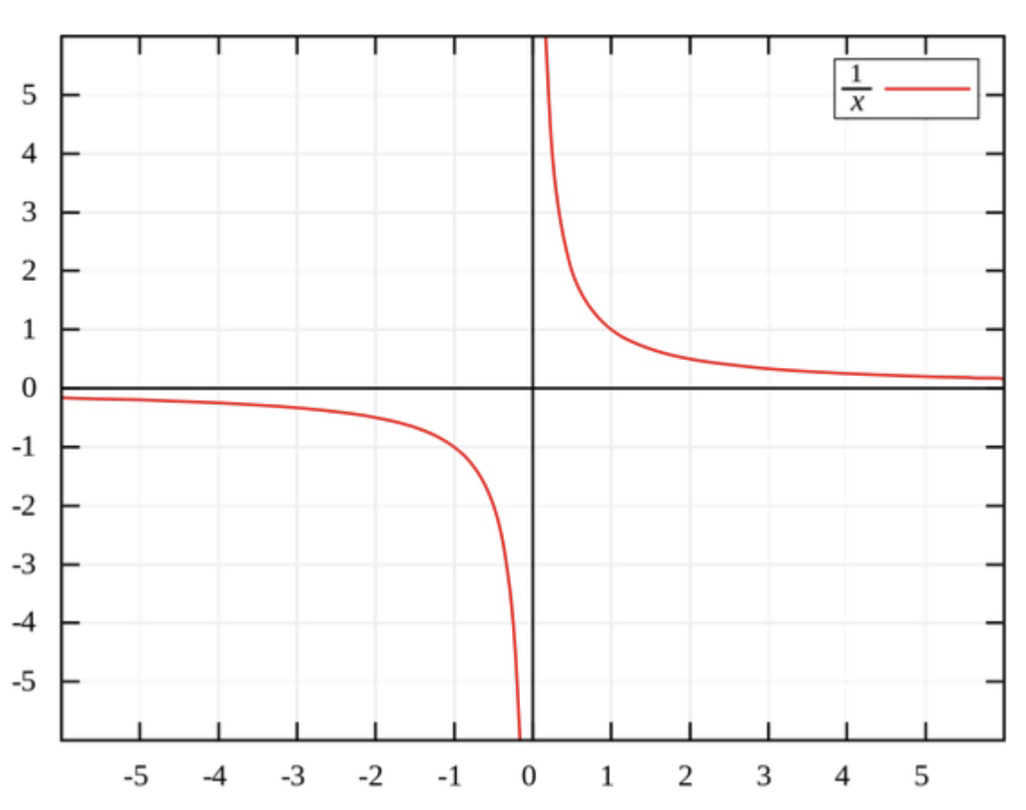
Additionally, if you take the limit of 1/x as x approaches zero from the positive side the result approaches positive infinity. If you take the limit from the negative side it approaches negative infinity.

An interesting thing to think about is whether multiplication by zero really makes much sense in the concrete world. You can’t really have zero groups of something. Zero groups of anything is still nothing. We can think of that abstractly once we have the abstract concept of numbers, but in the real world that idea is nonsense.

The key is understanding how divisions between 0 and 1 work. Say you take 2/0.5, you end up with 4. 2/0.25 you end up with 8. As you can see, those numbers get big fast. 1/0.0001 is 10,000.

As you approach 0, you get increasingly large numbers. If you flip it negative, again as you approach -0, you have increasingly big negative numbers. As you approach 0 from both sides, you approach positive and negative infinity. But what goes in the middle, at exactly zero? We don’t know, There’s no sensible value there, so it’s considered to be undefined.

In computers, it’s usually either an error, or represented with NaN (Not a Number) when you want to avoid throwing an error condition. NaN is defined so that any operations involving NaN is also NaN, so your entire equation becomes NaN.

Easiest way to visualize that is to input y = 1/x in a graph calculator (Desmos is nice). You clearly see it going to negative infinity then back at positive infinity.

With some other operations like negative square roots, we’ve made up the imaginary number i, which is defined to be the square root of -1, and we can make it do useful things. But what can we reasonably do with the result of dividing by zero? It behaves like infinities: you can’t really add or multiply them, or divide them. You’re just stuck with it. It’s impossible to represent, it’s Not a Number.

There are some good answers here already. I feel the need to add something, though.

If I gave you a number, 6, and multiplied it by 2 you’d get 12. If I asked you to “undo” the multiplication, you’d divide it by 2. So, you can think of division as the “inverse” of multiplication.

So: 12 * 1/2 = 6.

6, when doubled is 12, and 12, when halved, is 6. You can never double 6 and get 14. We say that multiplication between two (nonzero) numbers has a one-to-one relationship.

Then, let’s say I asked you what 0*6 is. And you’d say 0*6=0.

Then, let’s say I didn’t know what we started with. I give you this equation and ask you to find a value for x:

0*x=0

What is x? X can be anything here, 1, 17, pi, all numbers work. You can even choose 0.

Could you try 0*x*1/0=? How would you choose one number to be correct?

There is no “undo” button here. 1/0 is meaningless because we can’t assign it a unique value. A math person would say, “0 has no multiplicative inverse”.

Trying to interpret math in non-abstract terms is often misleading and just creates confusion. a/b is a solution to the equation bx = a, nothing more, nothing less. Then maybe you can use it to model a real-life situation, maybe not.

Dividing by zero is undefined in the realm of real numbers and basic arithmetic because there’s no meaningful answer. It’s not an abstract concept; it’s simply mathematically impossible due to the nature of division.

This clicked for me when my teacher explained it in terms of slopes.

The video here breaks it down nicely. https://virtualnerd.com/sat-math/geometry/slope/infinite-slope-definition.

So you have a vertical line with an infinite slope. There are no changes in x as you traverse the line, only changes in y. Or said differently, the line is described entirely by a single x-value which corresponds to every possible y-value.

If you think of it in terms of a function, it’s extremely problematic because you no longer have a mapping of a single y-value to each x-value. This violates the requirements of a function. It’s not possible to define the slope value when rise/run is something/zero, therefore we describe the function value as “undefined”.

But even though we can’t calculate a slope or address it with a function, it’s pretty easy to visualize and understand a vertical line. So that’s what dividing by zero represents in concrete terms.

Explain what exactly?

You can divide 2 apples between two people, or between four people, but you can’t divide them between zero people. That premise doesn’t make sense, the question is incomplete to be answerable.

By expanding our scale with another dimension (complex numbers in math) we expand the question. How do we add another dimension to the physical, practical anecdote? 🤔

You can cut something into 2 pieces, or 1 piece, but you can’t cut something into 0 pieces.

I am surprised that nobody pointed out that there is a mathematical structure where you can divide by zero, the wheel:

https://en.wikipedia.org/wiki/Wheel_theory?wprov=sfla1

Well, outside of the abstract realm, we never have exact, certain quantities. Even when counting objects. So when we devide by a very small quantity that we can approximate with the number 0, the outcome varies from some large number off the scale up to infinity, or some very low negative numbers, again off the scale and down to negative infinity. Since the range of valid answers to _1/0 is off the charts, we just say undefined instead.

You can also try doing some stuff with ohms law, you’ll see how hard it is to reach exactly 0 on the denominator.

I guess if I were to spill over to the non-numerical and semantical or more linguistically axiomstic representation here,:

1. The divisor is a number (1)
2. The dividend is a number (0)
3. A number divided by another number consequently produces another number
4. Does mathematics line up with CS on the whole NaN designation? I might be conflating fields or… I dunno. I’m sure there’s a palpable issue here you guys can lead this ass to override whatevers going on in my head